Introduction

The Gaussian distribution, also known as the normal distribution, is one of the most important and widely used probability distributions in statistics and data analysis. It provides a mathematical framework to describe and analyze continuous data that follows a bell-shaped curve. In this comprehensive blog, we will explore the intricacies of the Gaussian distribution, from its visual representation to the underlying mathematical formula, shedding light on its significance in various fields.

Understanding the Gaussian Distribution

The Gaussian distribution is characterized by its bell-shaped curve, which is symmetric around the mean. It is fully defined by two parameters: the mean (μ) and the standard deviation (σ). The mean represents the central location of the distribution, while the standard deviation measures the spread or dispersion of the data.

Visualizing the Gaussian Distribution

The shape of the Gaussian distribution can be visualized using probability density functions (PDFs) and cumulative distribution functions (CDFs). Let's delve into each visualization technique:

a) Probability Density Function (PDF): The PDF represents the probability of observing a particular value within a range of the distribution. For a Gaussian distribution with mean μ and standard deviation σ, the PDF is given by the formula:

f(x) = (1 / (σ * sqrt(2π))) * exp(-((x - μ)^2 / (2 * σ^2)))

This equation calculates the probability density at a specific value x. The curve reaches its maximum at the mean (μ) and decreases symmetrically as values move away from the mean.



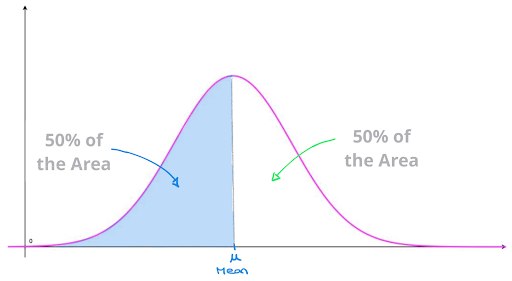
b) Cumulative Distribution Function (CDF): The CDF provides the probability that a random variable takes on a value less than or equal to a given value. It represents the cumulative area under the PDF curve. The CDF for a Gaussian distribution is not expressed in a closed form, but it can be approximated using numerical methods or lookup tables.

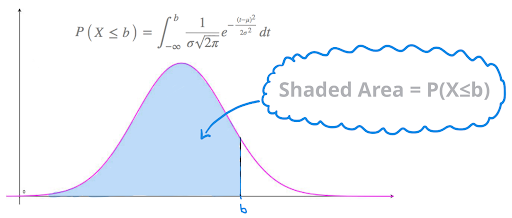
Properties of the Gaussian Distribution

The Gaussian distribution possesses several notable properties that make it widely applicable in various fields:

a) Central Limit Theorem: One of the key properties of the Gaussian distribution is its association with the Central Limit Theorem (CLT). According to the CLT, the sum or average of a large number of independent and identically distributed random variables tends to follow a Gaussian distribution, regardless of the shape of the original distribution. This property enables the Gaussian distribution to model real-world phenomena effectively.

b) Symmetry and Skewness: The Gaussian distribution is symmetric, meaning the curve is evenly distributed around the mean. This symmetry implies that the mean, median, and mode of the distribution coincide at the center. Additionally, Gaussian distributions have zero skewness, indicating a balanced distribution without a preference for one tail over the other.

c) Standardization and Z-Scores: Standardizing data is a common technique that involves transforming values to a standard Gaussian distribution with a mean of zero and a standard deviation of one. This process is achieved by calculating Z-scores, which represent the number of standard deviations a given value is away from the mean. Standardization simplifies comparison and analysis across different datasets.

Applications of the Gaussian Distribution

The Gaussian distribution finds extensive applications in various fields due to its versatility and mathematical properties. Some key applications include:

a) Statistical Inference: The Gaussian distribution forms the basis for many statistical inference methods, such as hypothesis testing, confidence intervals, and regression analysis. These techniques rely on assumptions of normality to make valid inferences about population parameters.

b) Financial Modeling: In finance, the Gaussian distribution is frequently used to model asset returns and market movements. It serves as a fundamental assumption in option pricing models, portfolio optimization, risk management, and the modeling of financial derivatives.

c) Quality Control: Gaussian distributions play a crucial role in quality control processes. By assuming that the measurements of a product or process follow a Gaussian distribution, statistical control charts can be created to monitor and detect deviations from the expected behavior. This helps identify anomalies and maintain the desired level of quality.

d) Machine Learning and Data Analysis: Many machine learning algorithms, such as linear regression and Gaussian mixture models, assume that the underlying data follows a Gaussian distribution. Gaussian-based models provide a solid foundation for data analysis tasks such as clustering, anomaly detection, and dimensionality reduction.

e) Natural Phenomena Modeling: The Gaussian distribution is often used to model various natural phenomena, such as the heights and weights of individuals in a population, noise in scientific measurements, and errors in experiments. Its ubiquity stems from the Central Limit Theorem, which suggests that many phenomena tend to follow a Gaussian distribution due to the aggregation of multiple independent factors.

Beyond the Standard Gaussian Distribution

While the standard Gaussian distribution is the most commonly used form, variations and extensions exist to handle specific scenarios:

a) Multivariate Gaussian Distribution: The multivariate Gaussian distribution extends the concept of the Gaussian distribution to multiple dimensions. It characterizes the joint probability distribution of multiple variables and allows modeling of correlations and dependencies between them.

b) Student's t-Distribution: The t-distribution is a variant of the Gaussian distribution that accounts for smaller sample sizes and potential outliers. It has heavier tails, allowing for increased robustness in the presence of extreme values.

c) Skewed Distributions: In some cases, real-world data may exhibit skewness or asymmetry. Skewed distributions, such as the log-normal distribution or the gamma distribution, provide alternatives to the standard Gaussian distribution for modeling such data.

Conclusion

The Gaussian distribution is a cornerstone of statistical analysis and plays a pivotal role in various fields, including statistics, finance, machine learning, and quality control. Its visual representation through probability density functions and cumulative distribution functions provides a powerful tool for understanding and analyzing continuous data. With its properties of symmetry, standardization, and association with the Central Limit Theorem, the Gaussian distribution serves as a fundamental framework for modeling and inference. By understanding and utilizing the Gaussian distribution, analysts and researchers can gain valuable insights and make more accurate predictions from their data.