In statistics and probability theory, the concept of Maximum Likelihood Estimation (MLE) stands as a powerful tool. MLE allows us to estimate the parameters of a probability distribution, enabling us to make informed decisions and predictions. In this blog, we will dive deep into the world of MLE, focusing specifically on its application to the Gaussian distribution, which is one of the most widely used distributions in various fields.

What is Maximum Likelihood Estimation?

MLE is a powerful and widely used statistical method for estimating the parameters of a probability distribution. It operates under the principle that the most likely values for the parameters are those that maximize the likelihood of observing the given data. In simpler terms, it seeks to determine the most plausible values for the parameters given the available data.

The goal of MLE is to find the values of the parameters that maximize the likelihood function or, equivalently, the log-likelihood function. This process involves solving an optimization problem, typically by finding the derivative of the log-likelihood function and setting it to zero.

Gaussian Distribution

Before we delve into MLE in the context of the Gaussian distribution, let's first understand what the Gaussian distribution represents. Also known as the normal distribution, it is a continuous probability distribution that describes the behavior of many real-world phenomena. It is

characterized by its bell-shaped curve, with the majority of the data clustered around the mean.

The Gaussian distribution is fully determined by two parameters: the mean (μ) and the standard deviation (σ). The mean represents the central location of the distribution, while the standard deviation determines the spread or dispersion of the data around the mean.

Maximum Likelihood Estimation with the Gaussian Distribution:

Now, let's explore how MLE can be applied to estimate the parameters of a Gaussian distribution using a simple example.

Let's imagine we have a dataset of heights, and we want to estimate the parameters of the Gaussian distribution that best fit our data. We start by making an assumption that our data follows a Gaussian distribution. This assumption is reasonable in many real-world scenarios, given the prevalence of the Gaussian distribution.

Step 1: Define the Probability Distribution:

Begin by selecting a probability distribution that you believe is appropriate for modeling your data. The choice of distribution depends on the characteristics of the data and the problem at hand. Common choices include the Gaussian (normal), exponential, binomial, and Poisson distributions. Here we will find the MLE of Gaussian Distribution.

In this equation, "x" represents the random variable, "μ" represents the mean (or expected value), and "σ" represents the standard deviation of the distribution. The PDF describes the relative likelihood of observing a specific value "x" from the distribution.

Step 2: Formulate the Likelihood Function:

Based on the selected probability distribution, write down the mathematical expression for the likelihood function. This function quantifies the probability of observing our data given specific parameter values.

In the case of the Gaussian distribution, the likelihood function L(μ, σ²) is defined as the joint probability density function of the observed sample. The likelihood function. Since the samples are independent and identically distributed, we can express the likelihood function as the product of individual pdfs:

Step 3: Take the Logarithm:

Having defined the likelihood function, the next step is to find the parameter values that maximize it. In practice, it is often more convenient to maximize the logarithm of the likelihood function, known as the log-likelihood function. Maximizing the log-likelihood function is mathematically equivalent to maximizing the likelihood function itself.

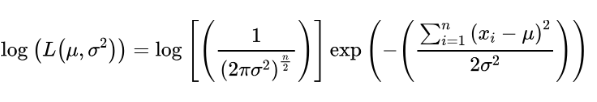
Using the properties of logarithms, we can separate the terms and simplify further:

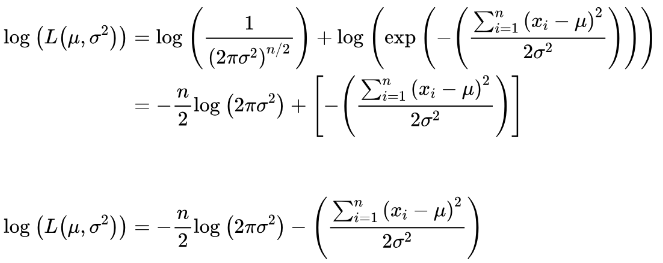
Step 4: Differentiate the Log-Likelihood Function and set the derivatives to zero. After this solve for the Parameter Values::

To find the values that maximize the log-likelihood function, we differentiate it with respect to the parameters (mean and variance), set the derivatives equal to zero, and solve for the maximum likelihood estimators (MLEs).

Setting the derivative(s) of the log-likelihood function to zero, identifying the critical points where the maximum likelihood occurs. Solving these equations will give you a system of equations, which may require algebraic manipulation or numerical techniques to solve.

For the Gaussian distribution, the MLE for the mean (μ) is the sample mean of the data, while

the MLE for the variance (σ²) is the sample variance.

Solve the system of equations obtained in the previous step to find the parameter values that maximize the log-likelihood function. The solutions to these equations represent the maximum likelihood estimates of the parameters.

Differentiating wrt μ:

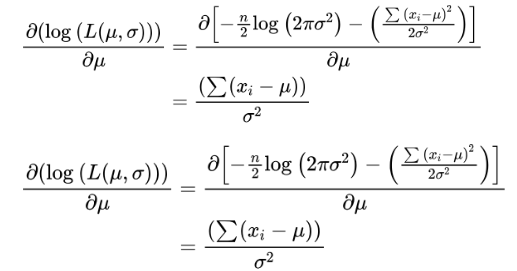
Setting this derivative equal to zero and solving for μ, we get:

Differentiating wrt σ²:

Setting this derivative equal to zero and solving for σ², we get:

Step 5: FInding the values of mean and standard deviation.

Finally, we can obtain the maximum likelihood estimate for σ by taking the square root of the estimated variance:

Thus, the MLE estimates for the parameters of a normal distribution are

Interpretation and Intuition:

Now that we have the MLEs for the mean and variance, what do they represent? The MLE for the mean is the best estimate of the average height in our dataset, while the MLE for the variance measures the spread or variability of the heights around the mean. These estimates allow us to understand and characterize the distribution of heights more accurately.

Maximum Likelihood Estimation is a powerful tool in the world of statistics that allows us to estimate the parameters of a distribution, such as the Gaussian distribution. By maximizing the likelihood function, we find the parameter values that make our observed data most likely. In the case of the Gaussian distribution, the MLEs for the mean and variance provide valuable insights into the central tendency and dispersion of the data.

Understanding MLE and its application to the Gaussian distribution equips us with the ability to analyze data and make informed decisions. Whether it's predicting stock prices, analyzing medical data, or understanding social phenomena, the mastery of MLE opens doors to a deeper understanding of the world around us. So, embrace the magic of MLE and unravel the mysteries hidden within your data!