1. Adjacency Matrix:

An adjacency matrix is a way to represent a graph using a two-dimensional matrix.

In an adjacency matrix, the rows and columns of the matrix represent the vertices of the graph. If there are n vertices in the graph, the adjacency matrix will have dimensions n x n. Each cell of the matrix represents an edge in the graph.

If there is an edge between vertex i and vertex j, the value at the cell (i, j) (and (j, i) for an undirected graph) is typically set to 1. If there is no edge between the two vertices, the value is usually set to 0. This way, the adjacency matrix provides a binary representation of the connections in the graph.

For example, consider a graph with 4 vertices: A, B, C, and D. The adjacency matrix for this graph would be:

A B C D

A 0 1 1 0

B 1 0 1 1

C 1 1 0 0

D 0 1 0 0

In this matrix, we can see that there is an edge between vertex A and vertex B, between A and C, between B and C, and between B and D.

1. Adjacency List:

An adjacency list is another way to represent a graph, and it is often more memory-efficient than an adjacency matrix, especially for sparse graphs.

In an adjacency list, each vertex in the graph is associated with a list (or array) that contains its neighbouring vertices.

For example, consider a graph with 4 vertices: A, B, C, and D. The adjacency list representation for this graph would be:

A -> B, C

B -> A, C, D

C -> A, B

D -> B

In this representation, for each vertex, we maintain a list of its neighbouring vertices. Vertex A is connected to vertices B and C, vertex B is connected to vertices A, C, and D, vertex C is connected to vertices A and B, and vertex D is connected to vertex B.

Implementation of Graph using Adjacency List:

CODE:

#include

#include

using namespace std;

class Graph{

list *adj;

int n;

public:

Graph(int s){

adj= new list [s];

n=s;

}

void addEdge(int u, int v, bool bidir=true){

adj[u].push_back(v);

if(bidir==true){

adj[v].push_back(u);

}

}

void print(){

cout<<”KEY”<<” ”<<”VALUE”<<endl;

for(int i=0; i<n; i++){

cout<<i<<”->”;

for(auto neighbor : adj[i]){

cout<<neighbor<<”->”;

}

cout<<”NULL”<<endl;

}

}

};

int main(){

Graph g(4);

g.addEdge(0,1);

g.addEdge(0,2);

g.addEdge(0,3);

g.addEdge(1,2);

g.addEdge(3,2);

g.print();

return 0;

}

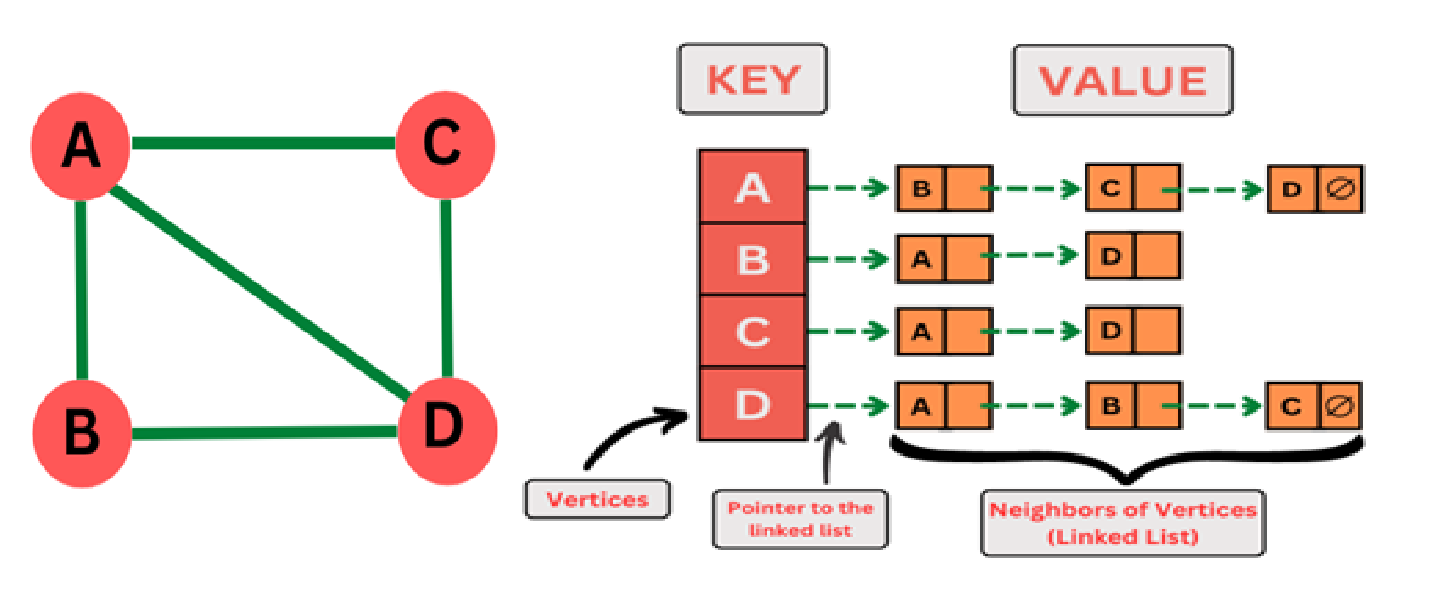
1. Hashmap:

A hashmap-based implementation of a graph involves using a hashmap data structure to represent the graph's adjacency list. The hashmap associates each vertex with a list of its neighbouring vertices.

Implementation of Graph using Unordered Map:

CODE:

#include

#include

#include<unordered_map>

using namespace std;

class Graph{

public:

unordered_map <string, list > adj;

void addEdge(string u, string v, bool bidir = true){

adj[u].push_back(v);

if (bidir == true){

adj[v].push_back(u);

}

}

void print(){

cout<<”KEY”<<” “<<”VALUE”<<endl;

for(auto p: adj){

cout<<p.first<<”->”;

for(auto neighbor : p.second){

cout<<neighbor<<”->”;

}

cout<<”NULL”<<endl;

}

}

};

int main(){

Graph g;

g.addEdge(“A”,”B”);

g.addEdge(“A”,”C”);

g.addEdge(“A”,”D”);

g.addEdge(“B”,”D”);

g.addEdge(“C”,”D”);

g.print();

return 0;

}

COMPARISON OF GRAPH REPRESENTATIONS:

|Representation|Structure|Flexibility|Space complexity|Time to add an edge| | :- | :- | :- | :- | :- | |Adjacency Matrix|Square matrix|Limited|O(V²)|O(1)| |Adjacency List|List of neighbouring vertices|Limited|O(V+E)|O(1)| |Edge List|List of edge tuples|Limited|O(E)|O(E)|